Entradas en "naturaleza"
Ruido Perlin
Vamos con una explicación (seguida por la implementación de rigor) del algoritmo de ruido más usado en todo el mundo; el ruido Perlin.
El modelo conceptual del ruido Perlin fue descubierto en 1982 por Ken Perlin como resultado de su trabajo de generación de texturas para la película Tron. Desde entonces, el ruido Perlin, y pequeñas variantes posteriores (como el ruido Simplex) son la base para generar efectos como fuego, humo, nubes… texturas como madera, mármol, granito… mapas de altura, etc, de forma totalmente automática. En esencia, nos permite generar patrones de forma muy similar a como lo suele hacer la naturaleza.
En esta entrada vamos a explicar todo el proceso, la naturaleza del ruido, a implementarlo, y finalmente a usarlo para generar terrenos en 3D como el de la siguiente imagen (y un visor interactivo para probarlos, al final de la entrada):
RUIDO BLANCO
Primero, entendamos las características del ruido aleatorio para comprender en qué se diferencia el ruido Perlin de él. Si generamos un mapa 2D de ruido blanco clásico (valores (pseudo)aleatorios), obtenemos algo similar a la siguiente imagen:
Exacto, es muy parecido a lo que veíamos en nuestras viejas televisiones cuando no habíamos seteado ningún canal; sólo que entonces era el resultado del ruido blanco electromagnético del ambiente, completamente caótico, y en este caso sólo son bits al azar.
¿Qué características importantes vemos en esa imagen?
1) Desde el punto de vista de la teoría de la información, la entropía es máxima. Así que esta imagen no puede comprimirse al codificarse sólo con los símbolos usados en su lenguaje (blanco/negro).
2) Desde un punto de vista físico, su densidad media es prácticamente constante (tiende fuertemente a serlo) para todos los fragmentos de dimensiones superiores a 1×1. Es decir, si hacemos un desenfoque gaussiano la imagen se volverá esencialmente plana, incluso con radios de tan sólo 2px.
RUIDO PERLIN (1 dimensión)
En el ruido Perlin las características son las opuestas, que es lo deseable cuando trabajamos en generación procedural o automática. Si entendemos cómo se crea el ruido, es fácil y lógico entender el por qué de esta naturaleza.
Así que empecemos:
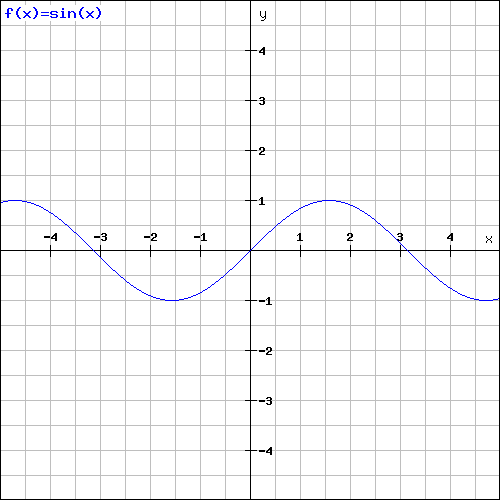
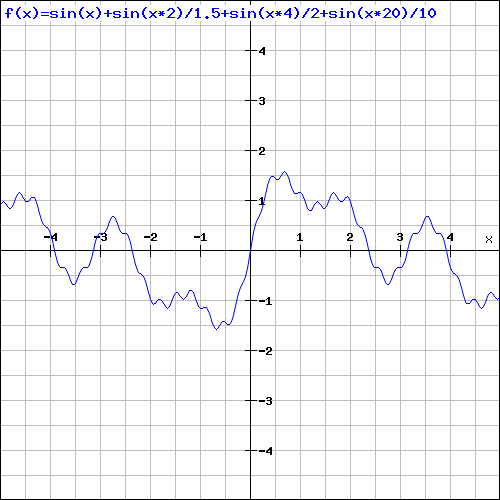
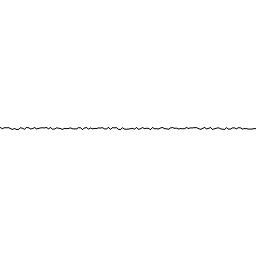
Vamos a calcular el ruido perlin como la generación de onda n-dimensional compuesta por k octavas. Si pensamos en la función seno para representar una onda:
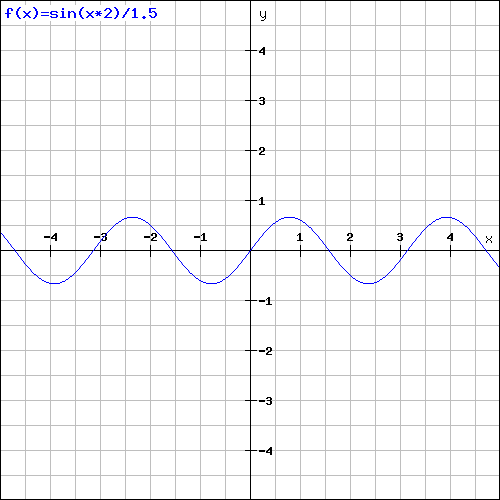
Vemos como su amplitud va desde -1 a 1 (2 en total) y su longitud de onda es 6. Esta bien podría ser la primera componente de nuestra onda final, en el siguiente paso, queremos una onda de la misma naturaleza, pero con mayor frecuencia (menor longitud de onda) y menor amplitud. Por ejemplo:
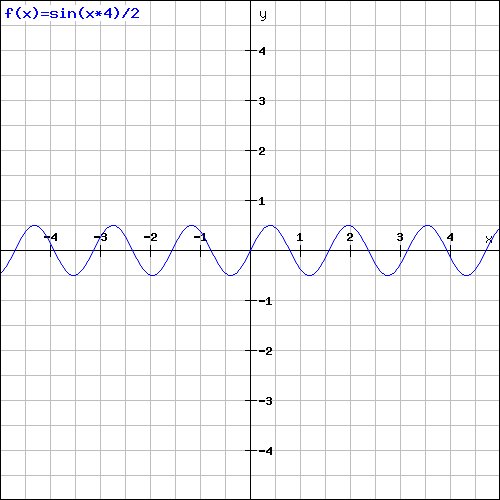
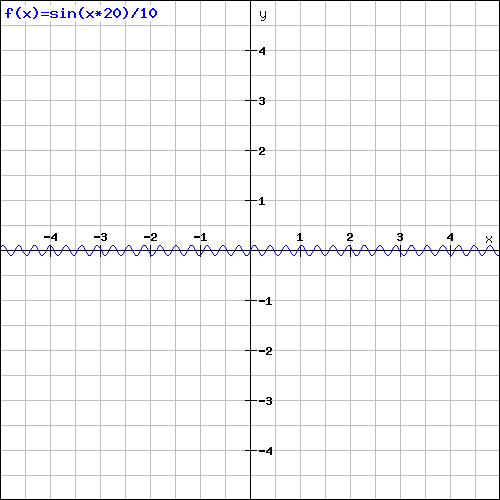
La tercera y cualta deberían obedecer al mismo principio (suponiendo que sólo usáramos 4):
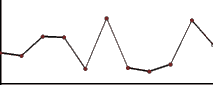
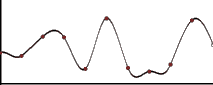
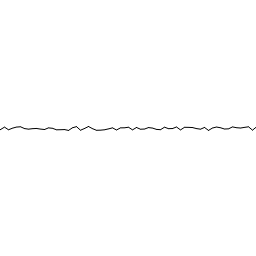
De esta forma, si sumamos las componentes anteriores, y en general cualesquiera en las que cada una aumenta la frecuencia y reduce la amplitud de forma progresiva, obtendremos algo como lo siguiente:
Esta onda unidimensional, que se asemeja al perfil de un paisaje montañoso cumple el siguiente principio, que tanto observamos en la naturaleza: A mayor escala, menor número de variaciones pero con más influencia, a menor escala, mayor número de variaciones pero con menor influencia. O dicho de otra forma, a altas frecuencias bajas amplitudes y viceversa.
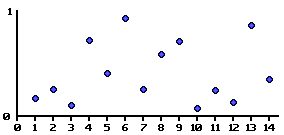
Pero en la naturaleza los procesos no están formados a base de ondas periódicas como el seno que hemos usado hasta ahora. Debemos crear una onda pseudo-aleatoria simplemente eligiendo valores aleatorios en los “nodos”. Los nodos son los puntos en los que una onda periódica alcanzaría un máximo o mínimo, es decir, debemos introducir valores cada λ unidades de espacio (longitud de onda).
Ejemplo:
puntos generadores aleatoriamente para generar una onda
Una vez generados los puntos, debemos interpolar entre los valores de los nodos para rellenar todo el dominio en el que se define la onda. Podemos usar aquí cualquier tipo de interpolación: linear, trigonométrica, Lagrange, B-splines… pero usualmente con una simple interpolación linear es suficiente. Los resultados finales no mejoran demasiado con interpolaciones más complejas (como los B-Splines, que sería la ideal) y que tienen un coste computacional muy alto. No obstante sois libres de usar la que mejor os parezca.
Nota: Tengo pendiente una entrada sobre interpolación, usando B-Splines (splines cúbicos) y Lagrange, que sí son muy útiles en otros cientos de aplicaciones.
interpolación lineal
interpolación por cosenos
interpolación cúbica
Para utilizar una nomenclatura adecuada, a cada componente vamos a llamarla octava, y usaremos un caso típico en el que en cada octava la frecuencia se multiplica por dos y la amplitud si divide por dos (de hecho, es así cómo se definen las octavas en música).
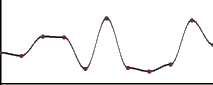
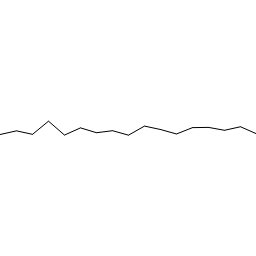
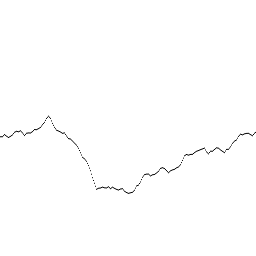
Con todo esto, ya podemos empezar a generar nuestra primera onda de ruido Perlin real. Empezaremos con una frecuencia de 2 (dos cambios en todo el dominio) y una amplitud de 128 (para representarla en una imagen de 256*256 siendo el centro del eje de ordenadas el centro de la imagen.
frecuencia: 2
amplitud: 128
frecuencia: 4
amplitud: 64
frecuencia: 8
amplitud: 32
frecuencia: 16
amplitud: 16
frecuencia: 32
amplitud: 6
frecuencia: 64
amplitud: 4
frecuencia: 128
amplitud: 2
El resultado de sumar estas 7 octavas es el siguiente:
Ruido Perlin final con 7 octavas
Y el código que he escrito para generarlas es el siguiente:
//=============
//Interpolation
//=============
var interpolate={}
interpolate.linear=function(x1,y1,x2,y2,x)
{
return ((x-x1)*(y2-y1)/(x2-x1))+y1;
}
//=============
//Perlin Noise
//=============
var perlin={}
perlin.octave(frequency, amplitude, length)
{
var wave=new Array(length);
var step_length=Math.floor(length/frequency);
for(var i=0;i<=length;i+=step_length)
{
//Create the nodes of the wave
wave[i]=(amplitude/2)-(Math.random()*amplitude);
//Interpolation between nodes
if(i>=step_length)
{
for(var j=i-(step_length-1);j<i;j++)
{
var x1=i-(step_length);
var x2=i;
wave[j]=interpolate.linear(x1,wave[x1],x2,wave[x2],j);
}
}
}
return wave;
}
Como veis el código es muy sencillo. El objeto “interpolate” está preparado para expandirse añadiendo nuevos métodos de interpolación si fuese necesario. Para generar todas las octavas y sumarlas, usando una progresión de doble frecuencia/mitad amplitud, podríamos simplemente hacer algo ad hoc como lo siguiente:
var lenght=256;
var perlin_wave=new Array(lenght);
var n_octaves=7;
for(var i=0;i<perlin_wave.length;i++) //wave initialization
perlin_wave[i]=0;
for(var i=1;i<=n_octaves;i++)
{
var current_pow=Math.pow(2,i);
var octave=perlin.octave(current_pow,lenght/current_pow,lenght);
for(var j=0;j<perlin_wave.length;j++)
perlin_wave[j]+=octave[j];
}
O bien, podemos crear un método dentro del objeto perlin con el código anterior si lo que queremos es tenerlo encapsulado.
Con esto ya tenemos nuestro generador de ruido Perlín en una dimensión. Aunque lo interesante viene para el caso en 2D.
Prueba a generar nuevas ondas con nuestra implementación haciendo clic en el botón
Generar una nueva onda
RUIDO PERLIN (2 dimensiones)
Para el caso de 2 dimensiones debemos pensar en la onda y sus octavas como mapas o texturas. Una octava 2D con frecuencia 2 creará dos valores aleatorios por dimensión, es decir, un total de 2×2=4 valores que estarán situados en las 4 esquinas del mapa. Si la amplitud es de 256 con valores entre -128 a 128 podemos normalizarla a valores entre 0 y 256 y dibujar en escala de grises (un gris para cada valor) la onda de forma muy gráfica y representativa.
Ejemplo:
En este caso, hemos rellenado el dominio vacío de la onda, con el color del punto definido que manda sobre el cuadrante; dado que como hemos dicho, sólo los vértices del mapa tienen un valor establecido. Sin embargo, lo ideal es de nuevo usar algún método de interpolación para rellenar todo el dominio. De nuevo el más usado para este caso es la interpolación lineal aplicada a dos dimensiones (bilinear), que está perfectamente explicada en la wikipedia. De esta forma, obtenemos algo como lo siguiente:
Usando estos principios, podemos empezar a generar octavas y crear nuestro ruido Perlin en 2D. Por ejemplo:
frecuencia: 2
amplitud: 128
frecuencia: 4
amplitud: 64
frecuencia: 8
amplitud: 32
frecuencia: 16
amplitud: 16
frecuencia: 32
amplitud: 8
frecuencia: 64
amplitud: 4
frecuencia: 128
amplitud: 2
La suma de todas estas octavas da como resultado:
Ruido Perlin 2D final con 7 octavas
Esta imagen ya tiene semejanza con algo que parecen ser nubes o humo sobre un fondo, de hecho, si dejamos el canal B a 255 y el canal G como el máximo de (185,valor_de_la_onda), habremos creado un sencillo filtro que produce imágenes como la siguiente:
nubes fluorescentes lanshóricas
El código para el ruido Perlin en 2D que he escrito para generar los ejemplos anteriores es el siguiente:
//=============
//Interpolation
//=============
var interpolate={}
interpolate.linear=function(x1,y1,x2,y2,x)
{
return ((x-x1)*(y2-y1)/(x2-x1))+y1;
}
interpolate.bilinear=function(x1,y1,x2,y2,v1,v2,v3,v4,tx,ty)
{
//P1:{x1,y1,v1} - P2:{x2,y1,v2} - P3:{x1,y2,v3} - P4:{x2,y2,v4}
//Target:{tx,ty}
//NOTE: Bind each area with the oposite value
var area_v1=Math.abs((tx-x1)*(ty-y1))*v4;
var area_v2=Math.abs((tx-x2)*(ty-y1))*v3;
var area_v3=Math.abs((tx-x1)*(ty-y2))*v2;
var area_v4=Math.abs((tx-x2)*(ty-y2))*v1;
var area_total=(x2-x1)*(y2-y1);
return (area_v1+area_v2+area_v3+area_v4)/area_total;
}
//=============
var perlin={}
perlin.octave_2d=function(frequency, amplitude, length)
{
var step_length=Math.floor(length/frequency);
var wave=new Array(length+1);
for(var i=0;i<=length;i++)
wave[i]=new Array(length);
for(var i=0;i<=length;i+=step_length)
{
for(var j=0;j<=length;j+=step_length)
{
//Create the nodes of the wave
wave[i][j]=(amplitude/2)-(Math.random()*amplitude);
//Interpolation between nodes
if(i>=step_length && j>=step_length)
{
for(var a=i-(step_length);a<=i;a++)
{
for(var b=j-(step_length);b<=j;b++)
{
var x1=i-(step_length);
var x2=i;
var y1=j-(step_length);
var y2=j;
wave[a][b]=interpolate.bilinear(x1,y1,x2,y2,wave[x1][y1],wave[x2][y1],wave[x1][y2],wave[x2][y2],a,b);
}
}
}
}
}
return wave;
}
//=============
function wave2D(data)
{
this.map=data;
this.add=function(data)
{
for(var i=0;i<data.length;i++)
{
for(var j=0;j<data.length;j++)
this.map[i][j]+=data[i][j];
}
}
this.render=function(ctx)
{
for(var i=0;i<this.map.length;i++)
{
for(var j=0;j<this.map.length;j++)
{
//Normalize from 0 to 255
var depth=Math.floor(128+this.map[i][j]);
//LaNsHoRic clouds: ("+depth+","+Math.max(185,depth)+",255)
ctx.fillStyle="rgb("+depth+","+depth+","+depth+")";
ctx.fillRect(i,j,1,1);
}
}
}
this.toURL=function()
{
var canvas=new Canvas();
canvas.width=canvas.height=this.map.length;
var ctx=canvas.getContext("2d");
this.render(ctx);
return canvas.toDataURL();
}
}
Con esto, podemos adaptar el código de generación anterior a lo siguiente:
var final_wave=new wave2D(perlin.octave_2d(1,256,256));
for(var i=1;i<8;i++) //7 octaves
{
var current_pow=Math.pow(2,i);
var octave=perlin.octave_2d(current_pow,256/current_pow,256);
final_wave.add(octave);
}
Prueba a generar nuevos mapas con nuestra implementación haciendo clic en el botón
Generar un nuevo mapa
Podemos cambiar la forma en que aumenta la frecuencia y disminuye la amplitud para obtener diferentes resultados. Jugando con la progresión y los valores podemos obtener texturas como granito, nubes dispersas, humo denso, etc. O usar el ruido como perturbación de un mapa base, con esto podemos generar lava, madera, mármol, relámpagos, etc. Sólo es cuestión de ir jugando con valores y experimentar un poco.
El siguiente uso popular de los mapas de ruido Perlin como el que acabamos de generar, es como mapas de altura. De esta forma podemos generar terrenos de forma automática, que en base a nuestros parámetros de generación podrán ser más o menos montañosos, más escarpados, más suaves…
En el siguiente cuadro puedes ver como usando nuestro generador de ruido Perlin creamos terrenos en 3D. Puedes hacer clic con el ratón y arrastrar para rotar la cámara. La implementación del modelado en 3D y del visor del mapa de altura están fuera del contenido de la entrada, pero prometo preparar una hablando de ello si os interesa (notificádmelo).
Como resumen rápido, dividimos un plano en tantas secciones de como frecuencia f tiene la mayor octaba. El plano queda con f*f vértices que asociamos con los píxeles del mapa 2D generado, para elevarlos según el valor del mapa en ese punto. Así el plano queda deformado como en los siguientes ejemplos:
Si os sirve de ayuda no es necesario mención pero sí sería cortés un agradecimiento aunque fuese en un comentario 🙂
Leer másConjunto de Mandelbrot
Dejo un pequeña “piece of code” de hace un par de años para generar el conjunto de Mandelbrot en un canvas con Javascript. Quería tener una imagen muy grande del conjunto con tonos azules, así que decidí generarla de la forma más rápida posible: un canvas y unas pocas líneas de código.
Fue una mala idea, descubrí entonces que la mayoría de navegadores soportan como máximo una dimensión en píxeles de 8192×8192 para el canvas; así que la imagen se limitaría como mucho a ese tamaño.
Descargar imagen final en tamaño completo
En cualquier caso… desde aquí podéis ejecutar el script; y el código (hecho ad hoc para generar la imagen y nada más):
var width=7500;
var height=width*0.88;
var canvas=document.getElementById("canvas");
var control=document.getElementById("control");
canvas.width=width;
canvas.height=height;
var context=canvas.getContext("2d");
var minAbsRe=-2.00;
var maxAbsRe=+0.80;
var minAbsIm=-1.25;
var maxAbsIm=+1.25;
var zoom=1;
var y=0;
function draw()
{
var minRe=minAbsRe*zoom;
var maxRe=maxAbsRe*zoom;
var minIm=minAbsIm*zoom;
var maxIm=maxAbsIm*zoom;
var reFactor=(maxRe-minRe)/(width-1);
var imFactor=(maxIm-minIm)/(height-1);
var maxIterations = 30;
var c_im=maxIm-y*imFactor;
for(var x=0;x<width;++x)
{
var c_re=minRe+x*reFactor;
var zRe=c_re, zIm=c_im;
var isInside=true;
for(var n=0;n<maxIterations;++n)
{
var zRe2=zRe*zRe,zIm2=zIm*zIm;
if(zRe2+zIm2>4)
{
isInside=false;
if(n<maxIterations/2)
context.fillStyle="rgb(0,0,"+(n*255/(maxIterations/2))+")";
else
{
var a=Math.round((n-(maxIterations*0.5))*255/(maxIterations/2));
var b=Math.round(a*Math.pow(n/maxIterations,3));
context.fillStyle ="rgb("+b+","+a+",255)";
}
context.fillRect(x,y,1,1);
break;
}
zIm=2*zRe*zIm+c_im;
zRe=zRe2-zIm2+c_re;
}
if(isInside)
{
context.fillStyle="#000";
context.fillRect(x,y,1,1);
}
}
if(y<height)
{
var progress=(y*100/height);
control.innerHTML=progress.toFixed(2)+"%";
y++;
setTimeout(draw,25);
}
else
{
var img=canvas.toDataURL("image/png");
control.innerHTML='<img src="'+img+'"/>';
}
}
Leer más
La visión en los perros
Llevo tiempo preguntándome cómo se ve el mundo desde los ojos de Arthur. Algunas personas piensan que los perros ven en blanco y negro, pero lo cierto es que sí distinguen algunos colores. En concreto, perros, lobos, zorros… y la mayoría de los cánidos y mamíferos poseen una forma de visión dicromática llamada deuteranopía; y es también, de hecho, una forma de daltonismo en humanos.
Los colores
Para entender nuestra visión: en la retina humana (y en la de muchos primates) podemos encontrar bastones (células de visión por intensidad) y tres tipos de conos (células responsables de la visión en color); cada tipo de cono especializado en una longitud de onda diferente: “azules” sensibles en un rango de longitudes centradas en el azul (unos 430nm), “verdes” especializados en longitudes de onda similares a la del verde (unos 520nm) y “rojos” para longitudes de onda largas cercanas al rojo (~650nm).
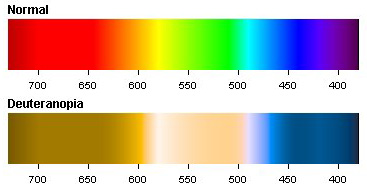
Dado que estas son las longitudes de los colores primarios aditivos (rojo – verde- azul); la composición de la información receptada por cada tipo de cono completa un espectro como el siguiente:
En los animales con deuteranopía los conos responsables de la recepción del verde no están presentes o no son funcionales. La composición de la información receptada presenta en estos casos un espectro como el siguiente:
Niveles de gris
Otra diferencia importante entre la visión humana y la de un perro es la diferencia mínima perceptible entre factores de gris (AR). Para esta medición se suele usar la ley de Weber-Fechner; una regla psicofísica que establece una relación cuantitativa entre la magnitud de un estímulo físico y cómo éste es percibido. El resultado de la fracción de Webber para humanos se estima en 0.11, y para perros en 0.22; esto significa que los perros son sólo capaces de captar la mitad de niveles de grises que nosotros.
Por ejemplo, los perros verían los siguientes cuadrados del mismo color:
Si tú ves el mismo color en ambos cuadrados, puede deberse a que tu monitor sea de gama baja y no sea capaz de mostrar correctamente los colores (o que esté mal configurado en parámetros de brillo, contraste y temperatura). Descartamos la opción de que seas un perro, claro.
Agudeza visual
Dicho en pocas (pero muy imprecisas) palabras; la agudeza visual es la resolución espacial del sistema visual. Al tratarse de un término de resolución es fácil imaginar que está directamente relacionado con la densidad de conos y bastones de la retina. Esta densidad varía según la zona; así, perdemos resolución en los límites de nuestro campo visual (donde apenas podemos percibir objetos) y alcanzamos el máximo en el punto donde centramos la vista.
El máximo de agudeza visual para humanos está entre 50 y 60 CPD. En los perros se sitúa entre 6.5-9 y 11.6 CPD.
Simular cómo es la visión con una agudeza visual diferente a la nuestra es complicado; intervienen muchos factores y es alterada circunstancialmente por el entorno. Por ejemplo el desenfoque por profundidad de campo se dispara (no podemos simularlo en una imagen 2D) al enfocar; y la cantidad de luz recibida también afecta de forma virtual; ya que los perros tienen mayor densidad de bastones que los humanos, pupilas más grandes y un tapetum lucidum refractivo; así en la oscuridad la agudeza visual de los perros acabaría superando a la del humano.
Aunque esta aproximación sea muy imprecisa; podemos ilustrar la pérdida de resolución con la siguiente figura; asumiendo un factor de /4 para los perros.
AV /1
AV /4
Al lío. Dedos al código.
Con todo este resumen; la idea es escribir una pequeña función javascript que dada una imagen de ejemplo la transforme y haga una aproximación acertada de cómo la percibiría un perro.
La función tiene 3 tareas independiente a realizar:
1) Simulación de deuterapía: No es tan sencillo como pueda parecer, ya que los niveles de luz y ponderaciones entre colores cambian gradualmente según la curva de sensibilidad de los conos que sí están presentes (rojo-azul). En este paper [1] encontramos los factores medidos experimentalmente -para humanos; aunque la diferencia con perros es mínima (comparamos con [2])- que necesitaremos para la conversión.
2) Discretizamos algunos niveles de luz. No vamos a implementar todas las curvas; sólo una aproximación. Algo de información adicional en [3]. Hacemos una reducción de la intensidad a niveles pares.
3) Desenfoque gausiano a la imagen. Para hacerlo correctamente el desenfoque variaría su grado arbitrariamente según la zona; y para ello necesitaríamos una imagen tridimensional, información sobre la exposición y el punto de enfoque marcado. Como no tenemos nada de eso, hacemos un desenfoque suave y global que simule el máximo grado de agudeza visual en todos los puntos. El desenfoque podemos hacerlo eficientemente (usando la GPU) mediante un filtro en CSS3 (fuera del código javascript).
function DogVision() //v0.1 - LaNsHoR @ 2014
{
//===================================================
//Factors
var gamma=1.0 /* normal value: 1.8;
-0.8 correction for dogs */
var by=127, k=[9591, 23173, -730];
for(var luts={}, invluts={}, i=0; i<256; i++)
{
luts[i]=0.992052*Math.pow(i/255, gamma)+0.003974;
invluts[i]=255*Math.pow(i/255, 1/1.8);
}
//===================================================
//Functions
//-- RGB normalization
function normalize(value)
{return value<0?0:value>255?255:value;}
//-- Dog light reduction
function even(value) {return value%2?value-1:value;}
//===================================================
this.dogPixel=function(r,g,b)
{
var r_lin=luts[r], g_lin=luts[g], b_lin=luts[b];
var r_blind=((k[0]*r_lin)+(k[1]*g_lin))/by;
var b_blind=((k[2]*r_lin)-(k[2]*g_lin)+32768*b_lin)/by;
r_blind=normalize(r_blind);
b_blind=normalize(b_blind);
var red=invluts[Math.round(r_blind)];
var blue=blue=invluts[Math.round(b_blind)];
return [even(red), even(red), even(blue)];
}
}
Y ya está! Podemos empezar a jugar con los resultados 🙂
Ejemplos
El resultado aparecerá en el rectángulo de borde azul.
Conclusión de andar por casa
Por todo lo dicho y visto; los perros en ambientes de luz diurna tienen una visión mucho más precaria que la humana. Sin embargo, con condiciones de baja luz su percepción de siluetas es mucho mejor que la nuestra (fijaos en los ejemplos). Además, su mayor número de bastones les hacen mejores detectando pequeños movimientos a grandes distancias (algo que no podemos percibir en imágenes estáticas).
No está nada mal. Después de todo; su sentido principal es el olfato (la mayoría de neuronas de su corteza cerebral están dedicadas a este sentido; la mayoría de las nuestras, a la visión). Aún con una visión mediocre, si sumamos sus excelentes olfato y oído su nivel de percepción sensorial global es superior al nuestro. Y desde luego, perfectamente adaptado a lo que necesitan.
Dedicatoria
Esta entrada y el código fuente de la función que hemos escrito están dedicados a Quarkyta… una de las preciosas perritas de Virgy, que nos dejó hace unos días 🙁
Referencias
[1] Digital Video Colourmaps for Checking the Legibility of Displays by Dichromats
[3] The spectral luminosity curves for a dichroma tic eye and a normal eye
Leer másAutómatas Celulares: Exposición 0
Un autómata celular (de ahora en adelante, CA) es un modelo matemático de un sistema dinámico cuyos estados evolucionan secuencialmente, de forma discreta (no difusa).
Probablemente encontréis algo similar a esta paupérrima definición en cualquier fragmento de literatura especializada que hable sobre el tema. Y digo paupérrima porque mi generosidad y magnanimidad me obliga a decir algo; como sabéis, en ningún caso la descripción de un fin o de una acción puede ser una definición -dado que, de hecho, hay otros “modelos matemáticos de un sis… blablabla” que encajan perfectamente con esa descripción, pero no son CA’s).
Yo siempre los he llamado “máquinas de estados basadas en memoria”. Examinemos su composición. Un CA está formado por:
1) Un espacio discreto de cualquier número de dimensiones que contendrá las células.
el más simple posible: una ristra de una dimesión
2) Un conjunto de células (en alguno de los estados definidos para el sistema)
dos estados: un ejemplo de “células-bits”
3) Una asociación que defina los vecinos de cada célula; usualmente… los adyacentes.
4) Una serie de reglas, que marcarán la evolución de cada célula.
Con todo esto; cada célula evolucionará dependientemente de sus vecinos e independientemente del resto del sistema; según las reglas que se hayan definido.
Generación 0
Generación 1
Generación 2
Supongamos que queremos que el estado de una célula dependa del estado de sus vecinas y del suyo mismo en la generación anterior. Gráficamente la regla podría representarse así:
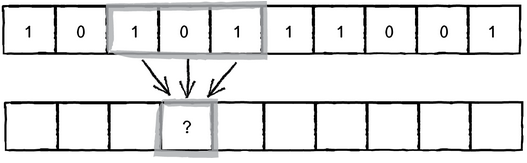
Definimos así 8 reglas, una por cada posibilidad:
El estado final es arbitrario, en este ejemplo hemos elegido éstos porque forman un CA muy simple que genera un resultado muy familiar… 😉
Los CA’s pueden usarse de múltiples formas para realizar cálculos de todo tipo. Un uso muy visual e instructivo para empezar consiste en usar una imagen de dimension W*H, donde W es el número de píxeles de ancho y el número de células del CA, cada fila de píxeles representa el CA en una generación concreta, y la fila siguiente se calcula en base a la anterior hasta un máximo de H generaciones.
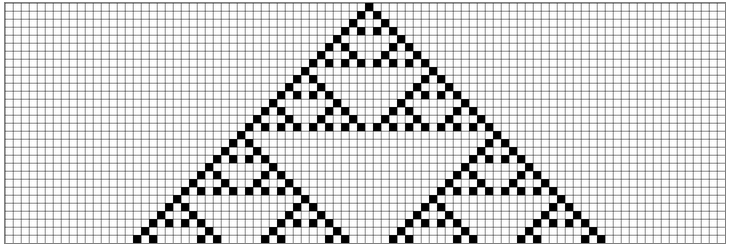
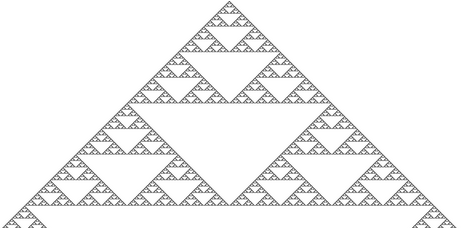
Por ejemplo, si el estado 0 es blanco y el estado 1 es negro, y creamos una imagen con un píxel negro en el centro de la primera fila, al ejecutar nuestro CA de ejemplo para calcular el resto de filas el resultado obtenido es el siguiente:
¿Os suena? Si hacemos un poco de zoom igual lo veis mejor… 😉
Efectivamente, es el triángulo de Sierpiński. Un fractral simple y muy conocido basado en división triangular; aunque nosotros lo hemos generado desde un CA…
Este es un ejemplo simple y rápido de cómo los CA’s pueden ayudarnos a sistematizar con un mínimo esfuerzo… modelos que se repiten en la propia naturaleza 🙂
