Sobre lambda lab 85
Si sólo vas a cambiar la sintaxis, podemos buscar un traductor… o crearlo. Un gigantesco autómata procesando la gramática con la que una vez se escribió el mundo. Seguro que no es tan difícil.
LaNsHoR
Supongo que lo mejor es abandonar la Tierra. En mi maleta mucha CocaCola de Vainilla y un laptop.
Un hogar de cera y miel
Este problema lo propuse el 20 de abril en Twitter. Mientras estaba en la playa. Es un problema muy sencillo, aunque sólo una persona de mi TL logró resolverlo… ( @erful )
Problema: En una teselación hexagonal regular, ¿cuál es la distancia entre dos circuncentros adyacentes en función del radio de una circunferencia cincunscrita a uno de los hexágonos?
* Sólo se necesitan matemáticas de la ESO… aunque sorprendente pocos acaban llegando a la solución correcta.
Problema (extra): Utiliza la solución para escribir una función en cualquier lenguaje de programación para dibujar sobre un buffer, plano, canvas, textura… una teselación como la del problema (dimensiones arbitrarias NxM).
* La solución la publicaré el domingo.
Leer másRompiendo la pared
Tercer problema, esta vez un poco de C++, y además muy fácil. Este es un problema clásico de mi carpeta de problemas a plantear en entrevistas de trabajo (yo personalmente nunca contrataría a alguien que no supiera resolverlo).
Este problema vino inspirado cuando, una vez, escuché a una persona A decirle a una persona B que no había forma de acceder a un miembro privado de una clase sin un getter, sin ser friend, etc…
Vamos a demostrarle todos a A que sí se puede:
class Locked
{
public:
int number;
private:
int secret;
public:
Locked() {number=-7;secret=85;}
};
int main()
{
Locked black_box;
int x = /* solución aquí */ ;
}
Tenemos un clase “Locked” con un entero público (number) y otro privado (secret). Tenemos que guardar en la variable “x” el valor del entero “secret” de la instancia “black_box” de la clase “Locked”. La solución cabe en una línea y por supuesto no puede escribirse nada fuera del main.
¿Voy abriendo ya la cerveza? 😀
Leer másProporciones Perfectas
¿Alguna vez os habéis sentido atrapados? Ya sabéis; recluidos. Confinados en una vida de la que no podéis escapar…
Pasan los años hasta que nos damos cuenta. Probablemente, cuando ya desesperados intentamos movernos y cambiar. Descubrimos entonces cómo la inercia de lo que hemos creído que somos y el pasado son unas duras cadenas. El entorno y la rutina se han convertido en las paredes de una celda y fortaleza que sólo nos deja expandirnos con límites. Vuestra evolución queda a merced de un espacio reducido; os perdéis las posibilidades del mundo entero… para vivir encerrados y casi sin opciones.
¿Os suena?
Claro, en informática a eso le llamamos sandbox.
Un entorno “cerrado” en el que los coders programan con los dedos mutilados. Os lo venderán como un invento maravilloso en pro de la seguridad; la celda ya no será celda, será un refugio. Todos aplaudirán y morirá la libertad. Al fin y al cabo, para los usuarios, la libertad es sólo un pequeño precio a pagar ante un escudo de papel que les proteja de su la falta de sentido común.
No estoy hablando de nada extraño o exótico. La web es exactamente esto; un ejemplo perfecto (y por desgracia, no el único).
Y de este tema, sobre las deficiencias del diseño de esta jaula aceptada y autoimpuesta diseñada desde la w3c (formada por el trío de estándares HTML, CSS, y JS) llega el problema de hoy, el segundo que os proponen los laboratorios lambda.
El problema:
Uno de los pilares del diseño web responsivo son las imágenes flexibles. Bajo este nombre, que intenta vanamente hacerse creer sofisticado, se esconde una idea muy simple: imágenes que escalan automáticamente en función del tamaño (anchura) de su padre en el DOM.
En principio una imagen se mostrará a su tamaño original, y si para ello tiene que “empujar” a su padre (por ejemplo un div) a ser más alto o más ancho, lo hará. Sin embargo, al poner la propiedad de CSS max-width:100% en la imagen, le estamos diciendo al navegador que esa imagen como máximo sea igual de ancha que su padre, así que ya no le empujará, y variará su tamaño en consecuencia cada vez que lo haga su padre (que deberá, junto a todos sus ascendientes, tener anchos relativos que se propaguen hasta el viewport).
Os he preparado un ejemplo en Fiddle (clic aquí). En el ejemplo tenéis 4 ventanas para código html, css, js y el resultado final. Probad a cambiar el tamaño de la ventana del resultado final para ver cómo la imagen cambia su tamaño al del padre en todo momento.
¿Notáis algo raro?
Efectivamente, el navegador está cambiando también la altura de la imagen aún cuando le hemos especificado que sólo cambie el ancho. Esto es porque el navegador sabe que la imagen tiene unas proporciones que se deben respetar, al cambiar el ancho, cambia también el alto, y con el alto de la imagen, cambia también el alto de sus padres, ya que no tienen un alto definido ni hay otros elementos que le “empujen” a tener más altura.
Cuestión:
Nosotros no tenemos libertad para definir comportamientos nuevos en CSS, y, por desgracia, no hay ninguna forma (directa) de especificar proporciones a elementos HTML de la misma forma que lo tienen las imágenes. El problema de hoy es crear un div con un aspect-ratio concreto (el que sea) y hacerlo “flexible” como si fuera una imagen, de forma que ocupe a todo su padre en anchura y su altura varíe automáticamente manteniendo siempre la proporción respecto a la anchura.
Os he preparado un ejemplo para que lo completéis aquí.
¿Parece fácil? No lo es 😉 Pero este ejercicio os ayudará a descubrir hasta que punto la cárcel es una cárcel.
Por supuesto está prohibidísimo usar javascript (nada de chapuzas). Solo CSS y HTML.
Venga, ¡¡a por él!!
*** SOLUCIÓN ***
Una vez más no tenemos ningún ganador… 🙁 Esta vez ni siquiera han habido soluciones propuestas. La cerveza prometida se está calentando… y algunos me habéis transmitido que no sabéis ni por donde empezar con este problema.
La solución la tenéis aquí (link). Probad a redimensionar la ventana a lo ancho (con la barra gris del centro de la página) para ver como el div escala manteniendo la proporción.
El código está en la solución, y lo comento rápidamente:
Necesitamos crear un contenedor auxiliar para nuestro div. Así que lo envolvemos en otro div “aux” en la solución. ¿Por qué? Porque este div auxiliar podrá controlar la altura en función de la anchura con la propiedad padding-top. En CSS, podemos poner un padding-top porcentual que será siempre relativo a la anchura del padre; de esta forma podemos jugar con un porcentaje que represente un aspect-ratio concreto (en nuestro ejemplo el padding-top es 50%, representa un aspect-ratio de 2:1; para un aspect-ratio tipo pantalla de PC panorámica (16:9) usaríamos 56.25% = 9/16*100).
Ahora tenemos un div auxiliar que marca las proporciones, pero no puede tener contenido porque toda su altura es de padding. La solución es marcarle su propiedad position como relative, y la del div original con contenido como absolute, junto a su top y a su left iguales a 0. También establecemos su ancho y altura iguales a las de su padre auxiliar dando valores de 100% a width y a height.
Con esto, tenemos el div “c” ocupando todo el div auxiliar que tiene, exactamente, el tamaño que queremos en todo momento; escalando según las dimensiones del viewport.
Leer másSé lo que estás mirando
Aquí el va el primer problema de algunos que iré proponiendo. Yo publicaré mi solución en unos días (4… o 5), dejando así un tiempo prudente ;]
/* si sois hábiles, no debería llevaros más que unos pocos minutos; pero en cualquier caso la velocidad no significa nada, lo importante es llegar a una buena solución; -es sobre todo un ejercicio mental, de diseño – */
Es muy sencillo pero, como nota, os diré que cuando vi la implementación de esto mismo en un proyecto grande… casi me echo a llorar.
***
Fue una de las primeras cosas que tuve que resolver hace algunos años para LoG85. Se trata de diseñar un fragmento del esquema de una base de datos para guardar, para cada usuario, qué publicaciones ha visitado y cuáles no. Las publicaciones pueden ser fotos, entradas, comentarios… lo que queráis, es lo de menos.
De partida tenemos una tabla usuarios y otra publicaciones, con los campos y restricciones que queráis; tenéis que conseguir que en la base de datos se guarden qué publicaciones han sido visitadas por qué usuarios. Tenéis libertad absoluta para crear o reformar tablas, escribir código, diseñar cachés… la película que queráis. Lo importante es que el sistema tiene que ser elegante (sencillo, claro, eficiente) y escalable (el número de usuarios y de publicaciones, así como su relación, puede crecer ad infinitum). Y por supuesto en todo momento la bd ha de encontrarse en un estado coherente; manteniendo la integridad referencial.
Si dais la solución en prosa, aseguraos de que todo está bien especificado 😉
*** SOLUCIÓN ***
¡Gracias a todos los que habéis participado! Bien vía comentarios, bien vía email o teléfono. Comento un poco las respuestas:
Todas las soluciones se han centrado en crear una tabla que representa la relación entre publicaciones y usuarios; las entradas de esta tabla nueva guardan qué usuarios han visitado qué publicación. Han habido diferentes versiones en las que se guardaban fechas, número de visitas, etc. Pero en cualquier caso, la versión básica de esta tabla, que sólo contendría dos claves ajenas a las primarias de las tablas usuarios y publicaciones, valdría (la primaria de la nueva tabla sería una composición de las dos ajenas).
Esta es la solución “trivial” que funciona. Pero no cumple uno de los objetivos del enunciado; no es escalable.
Primero, hablaremos de volumen; en un proyecto mediano que tenga unos 20.000 usuarios, es fácil que en pocos meses esos usuarios hayan visto una media de 1.000 publicaciones (fotos, tweets, entradas… lo que sea). Esto significa que nuestra tabla auxiliar tendrá 20.000.000 de filas. Y lo que es peor, crece geométricamente conforme aumenta el número de publicaciones y usuarios; a n*m. En pocos años tendremos una tabla con varios cientos de millones de filas, sólo para almacenar quién ha visto qué.
Aunque SGBD’s grandes tipo MySQL, MariaDB, Oracle… se comportan relativamente bien con tablas grandes, también tenemos que contemplar la posibilidad de que nuestra aplicación pueda correr sobre sistemas de gestión de bases de datos más modestos como SQLite. No sólo eso, para tener una velocidad aceptable es imprescindible tener los segmentos de las tablas más utilizados cacheados en RAM; con tablas tan grandes estamos invalidando la caché casi en cada consulta; llegado cierto punto límite en el que la tabla no quepa en memoria el rendimiento bajará de golpe varios órdenes de magnitud. Un diseño como este puede ser la diferencia entre que una aplicación vaya como un rayo en un hosting compartido o requiera un servidor dedicado entero para medio-funcionar. Y por supuesto, no podríamos ni plantearnos usar un sistema de instancias virtuales tipo Amazon, donde pagamos por consumo de memoria y ciclos de CPU.
La información mínima:
Este problema es peligroso porque es trivial encontrar una solución que “funciona”. Es fácil comformarse. Funciona en un “programa juguete” de estar por casa; pero muere en un entorno real. Tampoco hay una solución directa, dado que la información que tenemos que almacenar es esta y aparentemente no podemos reducirla más.
¿No podemos?
En realidad sí, y aquí está la magia.
Mi solución es usar una tabla “views” para las relaciones de esta forma:
| id_user | secuence_start | secuence_end |
|---|---|---|
| 34 | 5 | 5 |
| 34 | 7 | 10 |
| 34 | 12 | 12 |
| 36 | 20 | 28 |
| 785 | 5 | 5 |
La idea es la siguiente: lo más probable que es un usuario visualice muchas publicaciones con ids consecutivos (fotos de un album, respuestas de una entrada, entradas consecutivas, etc). Aún en el caso de que por la naturaleza de nuestra aplicación esta estadística no fuera cierta, más adelante veremos como forzar a que así sea.
Sabiendo esto, podemos explotar esta característica para almacenar segmentos de ids visitados, con un inicio y un final. Es decir, guardamos cosas como “el usuario 34 ha visitado todas las publicaciones de la 7 a la 10”.
A esto, añadimos un pequeño algoritmo de inserción, el consumo de CPU en la inserción es despreciable frente al consumo de CPU que supone consultas en una tabla cargada; además la inserción será una operación poco habitual.
Consulta para saber si una publicación ha sido visitada:
select true from views where id_user=$id_user and
secuence_start<=$id_post and secuence_end>=$id_post;
Algoritmo de inserción:
1) Comprobar si la publicación ya ha sido leída con la consulta anterior. Si es así, terminamos aquí.
2) Ejecutar:
update views set secuence_start=$id_post where
id_user=$id_user and secuence_start=$id_post+1;
Es decir, si queremos insertar como vista la publicación 6, y tenemos un segmento que empieza en la 7 para ese usuario, simplemente cambiamos el 7 por un 6.
El driver nos devuelve el número de filas cambiadas después de la operación, si es uno (se ha encontrado un segmento que cambiar), vamos al paso 2A. Si es cero, saltamos al 3.
2A) Comprobamos si el nuevo inicio de segmento es inmediatamente posterior a un final de segmento. Esto implica fusionar y desfragmentar segmentos que deben ser uno solo.
select secuence_start from views where id_user=$id_user
and secuence_end=$id_post-1;
Guardamos el resultado en una variable $tmp. Si $tmp tiene valor (hay resultado), actualizamos el segmento siguiente y eliminamos el que quedará con información redundante:
update views set secuence_start=$tmp where id_user=$id_user and secuence_start=$id_post; delete from views where id_user=$id_user and secuence_start=$tmp and secuence_end=$id_post-1;
Hemos terminado nuestra inserción y fusión 🙂
3) Ejecutar:
update views set secuence_end=$id_post where
id_user=$id_user and secuence_end=$id_post-1;
Es lo mismo que la operación anterior, pero para los finales de segmento. Preguntamos al driver el número de filas modificadas. Si es uno, pasamos a 3A, si no a 4.
3A) Repetimos las operaciones en 2A por el mismo motivo, adaptadas a una inserción de final de segmento.
select secuence_end from views where id_user=$id_user and secuence_start=$id_post+1; --guardado en variable tmp update views set secuence_end=$tmp where id_user=$id_user and secuence_end=$id_post; delete from views where id_user=$id_user and secuence_start=$id_post+1 and secuence_end=$tmp;
Terminada la inserción y fusión.
4) Llegados a este punto, no hay ningún segmento para el que nuestra entrada vaya a formar parte.
Ejecutamos:
insert into views values($id_user,$id_post,$id_post);
Y fin.
En cuanto pueda os pondré números reales de lo que supone realmente este algoritmo en rendimiento y reducción de tablas; basándome en la bd de log85 😉
¿Cómo llegué a esta solución?
Esto es lo más importante; la verdadera lección de este problema. A menudo tenemos que trabajar con cantidades enormes de información que no podemos comprimir en base a su grado de entropía usando métodos tradicionales.
Pero, como mentes inteligentes y cumbres del pensamiento abstracto que somos (nos queremos), debemos aprovechar nuestra condición humana para encontrar patrones y características que vuelvan a esa información vulnerable. Ya no en almacenamiento; en procesamiento cualquier “información sobre la información” que nos restrinja de una entrada de palabras aleatorias puede marcar la diferencia entre encontrar un algoritmo que se ejecute en 100ms, o tener que usar otro “default” que necesitará, literalmente, varios cientos años para darnos una respuesta.
Esta es sólo una idea. Puede mejorarse sobre la misma base y forzar la estadística para que los ids de lo que ven los usuarios sean más secuenciales. Por ejemplo; las entradas pueden tener ids como 100, 200, 300, 400… y los comentarios a las entradas como unidades sumadas a la id de la entrada: 101, 102, 103… así al ver entradas y comentarios tenemos un buen segmento asegurado. Esto no significa un límite de 100 comentarios por entradas. Cuando nos quedemos sin ids para la secuencia podremos romperla… al fin y al cabo, lo único importante de un id es que sea único (no necesariamente secuencial). Podéis jugar con esto para reducir la fragmentación entre ids de lo que realmente se ve.
Si lo probáis, veréis como la mejora con esta solución es espectacular. Espero que os haya gustado 🙂
Leer másIntersección Rayo-Triángulo
Hagamos un poco de abstract:
La intersección rayo-triángulo en R3 es un problema clásico que a menudo nos encontramos cuando buscamos soluciones a un sistema que depende de la topología de una malla triangular que interactúa con otra entidad en la escena. Especialmente en aplicaciones y variaciones de raytracing tipo mapeado fotónico; esto es, para renders offline.
 frame de Big Buck Bunny, renderizado con Blender
frame de Big Buck Bunny, renderizado con Blender
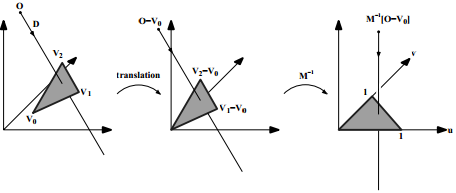
Hay muchas técnicas para calcularla, una casi omnipresente y eternamente recomendada es la Intersección Rayo-Triángulo Rápida de Mínimo Almacenamiento de Moller y Trumbore (conocida como MT97); basada en el cambio de coordenadas baricéntricas del triángulo en cuestión.
El paper del último link de MT97 explica bien el algoritmo y proporciona una implementación. Probablemente, es la que necesitáis para vuestro problema.
¿Probablemente?
Lo mejor de MT97 es que nos da una valiosa lección de filosofía. Su defecto, como el de tantas cosas en la vida, es el de su adopción masiva sin planteamiento.
Más que en ningún otro sitio, en este tipo de problemas hay que ser especialmente crítico; sobretodo en las líneas clave que van a suponer más del 70% del código de ejecución (no fuente) del programa.
Así, hace algunos años cuando me encontré con la necesidad de implementar una solución para calcular la intersección rayo/triángulo hice una comparativa (cosas de la intuición) entre MT97 y mi opción alternativa. Sorprendentemente encontré que para mi problema era mucho más rápida (computacionalmente) esta última.
La primera ventaja que intuí antes de hacer la prueba venía por su naturaleza paralelizable. Programándola usando instrucciones SSE y registros XMM* en gran parte del proceso obtenía hasta tres operaciones por instrucción.
El algoritmo es el siguiente:
- Calcular la intersección del rayo con el plano que define el triángulo (problema mucho más sencillo y bien conocido -se da en matemáticas de bachillerato <o al menos yo lo dí>-).
- Sumar las áreas de los tres triángulos formados al unir los vértices del triángulo original con el punto de intersección (si el rayo es aproximado o totalmente paralelo al plano, terminamos aquí).
- Sumar las áreas de los tres triángulos formados y calcular el área del triángulo original.
Se puede demostrar matemáticamente que si la suma de las tres áreas de los formados es igual a la del original, entonces el punto de intersección está dentro del original. Dando como trivial el punto 1, nuestro problema se reduce pues a calcular el área de un triángulo en R3.
La función implementada y con comentarios en español quedaría:
/*
Los registros XMM* son de 128bits, utilizo 4 floats
para llenarlos en una estructura V4.
*/
struct V4
{
float a;float b;float c;float d;
V4(float x=0){a=b=c=d=x;}
V4(float x, float y, float z, float i){a=x;b=y;c=z;d=i;}
};
/* P*: Vértice *(x,y,z) - R: Resultado */
void inline AreaOfATriangle(V4& P1, V4& P2, V4& P3, V4& R)
{
V4 DIV(0.5);
//Nota: Las coordenadas .d deben ser 0
//TODO: Setear a 0 estos últimos 32bits para P1, P2 y P3
asm volatile
(
"MOVUPS %0, %%XMM1\n\t" //Sube x,y,z de P1 a XMM1
"MOVUPS %1, %%XMM2\n\t" //Sube x,y,z de P2 a XMM2
"MOVUPS %2, %%XMM3\n\t" //Sube x,y,z de P3 a XMM3
"MOVUPS %%XMM2, %%XMM4\n\t" //Copia P2 en XMM4
"SUBPS %%XMM1, %%XMM4\n\t" //Resta P2-P1 (XMM4)
"MOVUPS %%XMM3, %%XMM5\n\t" //Copia P3 en XMM5
"SUBPS %%XMM1, %%XMM5\n\t" //Resta P3-P1 (XMM5)
//--- Producto vectorial de P2P1 y P3P1 (determinante 3x3)
"PSHUFD $0xC9, %%XMM4, %%XMM6\n\t" //P2P1 en XMM6 (Y,Z,X)
"PSHUFD $0xC9, %%XMM5, %%XMM7\n\t" //P3P1 en XMM7 (Y,Z,X)
"MULPS %%XMM4, %%XMM7\n\t" //P2P1 * P3P1(Y,Z,X)
"MULPS %%XMM5, %%XMM6\n\t" //P3P1 * P2P1(Y,Z,X)
"SUBPS %%XMM7, %%XMM6\n\t" //Resta XMM6 y XMM7
//--- Módulo del vector resultado
"MOVUPS %%XMM6, %%XMM7\n\t" //Resultado a XMM7
"MULPS %%XMM6, %%XMM7\n\t" //Cuadrado de componentes XMM7
"HADDPS %%XMM7, %%XMM7\n\t" //Suma parcial de coordenadas
//... (A+B,C+D,A+B,C+D)
"HADDPS %%XMM7, %%XMM7\n\t" //Fin la suma
//... ((A+B)+(C+D),...)
"SQRTPS %%XMM7, %%XMM7\n\t" //Raíz cuadrada del resultado
"MOVUPS %3, %%XMM6\n\t" //Sube 0.5 a XMM6
"MULPS %%XMM6, %%XMM7\n\t" //Divide el resultado entre 2
"MOVUPS %%XMM7, %4" //Pone el resultado en R {R(0)}
:"=m"(P1), "=m"(P2), "=m"(P3), "=m"(DIV), "=m"(R)
:"m"(R)
);
return;
Como siempre lo mejor es hacer pruebas en las máquinas que vayan a ejecutar el código. Gran parte de la mejora en velocidad viene del hecho de reducir los accesos a memoria (todo lo que sea pasearse por el bus de la placa base es siempre como subirse a una tortuga…) y no salir de los registros de la CPU.
De esto hace ya algunos años, la extensión SSE4.2 incluye una instrucción para calcular el producto vectorial (nos ahorramos 5 instrucciones en el código dado). Si la integráis con la intersección plano/triángulo y la adaptáis a una CPU contemporánea de gama alta, vuestro raytracer podrá casi volar… 😉
Leer más$blog->run();
Carl Sagan
Leer más