Conjunto de Mandelbrot
Dejo un pequeña “piece of code” de hace un par de años para generar el conjunto de Mandelbrot en un canvas con Javascript. Quería tener una imagen muy grande del conjunto con tonos azules, así que decidí generarla de la forma más rápida posible: un canvas y unas pocas líneas de código.
Fue una mala idea, descubrí entonces que la mayoría de navegadores soportan como máximo una dimensión en píxeles de 8192×8192 para el canvas; así que la imagen se limitaría como mucho a ese tamaño.
Descargar imagen final en tamaño completo
En cualquier caso… desde aquí podéis ejecutar el script; y el código (hecho ad hoc para generar la imagen y nada más):
var width=7500;
var height=width*0.88;
var canvas=document.getElementById("canvas");
var control=document.getElementById("control");
canvas.width=width;
canvas.height=height;
var context=canvas.getContext("2d");
var minAbsRe=-2.00;
var maxAbsRe=+0.80;
var minAbsIm=-1.25;
var maxAbsIm=+1.25;
var zoom=1;
var y=0;
function draw()
{
var minRe=minAbsRe*zoom;
var maxRe=maxAbsRe*zoom;
var minIm=minAbsIm*zoom;
var maxIm=maxAbsIm*zoom;
var reFactor=(maxRe-minRe)/(width-1);
var imFactor=(maxIm-minIm)/(height-1);
var maxIterations = 30;
var c_im=maxIm-y*imFactor;
for(var x=0;x<width;++x)
{
var c_re=minRe+x*reFactor;
var zRe=c_re, zIm=c_im;
var isInside=true;
for(var n=0;n<maxIterations;++n)
{
var zRe2=zRe*zRe,zIm2=zIm*zIm;
if(zRe2+zIm2>4)
{
isInside=false;
if(n<maxIterations/2)
context.fillStyle="rgb(0,0,"+(n*255/(maxIterations/2))+")";
else
{
var a=Math.round((n-(maxIterations*0.5))*255/(maxIterations/2));
var b=Math.round(a*Math.pow(n/maxIterations,3));
context.fillStyle ="rgb("+b+","+a+",255)";
}
context.fillRect(x,y,1,1);
break;
}
zIm=2*zRe*zIm+c_im;
zRe=zRe2-zIm2+c_re;
}
if(isInside)
{
context.fillStyle="#000";
context.fillRect(x,y,1,1);
}
}
if(y<height)
{
var progress=(y*100/height);
control.innerHTML=progress.toFixed(2)+"%";
y++;
setTimeout(draw,25);
}
else
{
var img=canvas.toDataURL("image/png");
control.innerHTML='<img src="'+img+'"/>';
}
}
Leer más
Atractores, caos, sistemas complejos y mariposas
Siempre nos sentimos más cómodos con aquello que creemos que conocemos; con aquello que ya sabemos y no puede cambiar. Pero en en realidad, siendo un poco puristas, la estabilidad no existe. Ningún sistema en la naturaleza (sistemas reales, no artefactos matemáticos imaginarios) es estable; en el sentido de que no va a permanecer inalterado para siempre. No existe nada en este universo, que haya detenido su evolución nunca.
En la práctica, cuando hacemos ciencia y estudiamos sistemas “aislados”, rebajamos considerablemente nuestros requisitos de estabilidad; y decimos que un sistema ha alcanzado la estabilidad cuando su evolución cesa durante “un tiempo lo suficientemente largo”.
Sí, es tan poco riguroso como suena…
Pero lo divertido está en la incertidumbre, y una vez perdemos el miedo a lo desconocido podemos empezar a disfrutar de ella. Veamos algunos tipos de sistemas con ejemplos sencillos y clasifiquémoslos:
Sistemas Simples
Un ejemplo de sistema simple es una taza de café caliente suspendida en una atmósfera de aire. Poco a poco la taza irá enfriándose hasta alcanzar la temperatura ambiente del aire (el sistema alcanzará la estabilidad). En sus inicios, el sistema no es estable, pero nos sentimos casi tan cómodos con estos sistemas como con los estables porque es fácil predecir su evolución.
Sistemas Complejos
Un sistema complejo es un sistema cuya evolución es muy difícil de determinar; ya que existen factores no evidentes que afectan de forma dramática a cómo evoluciona el sistema. Un ejemplo es el campo gravitatorio, cuando hay varios cuerpos en juego y en movimiento; es difícil calcular la evolución de las trayectorias.
Para verlo mejor; he escrito un pequeño script para hacer simulaciones (del que hablaremos después). En la primera simulación tendréis 6 puntos negros que representan cuerpos “fijos” que atraen a otro “móvil” cuya trayectoria queda marcada por una estela azul. La simulación es infinita y no se estabiliza nunca (aunque durante un rato el objeto móvil se salga de la pantalla, tarde o temprano volverá).
Para empezar la simulación haced clic en “empezar simulación” (podéis reiniciarla cuando queráis). ¿Podéis calcular mentalmente su trayectoria (la evolución del sistema)? Entonces, es un sistema complejo. Otro ejemplo de sistema complejo es el clima de la tierra.
Sistemas Caóticos
Un sistema caótico es un sistema, que además de complejo, cumple la siguiente propiedad fundamental: un mínimo y casi insignificante cambio en las condiciones iniciales hace que el sistema evolucione de forma radicalmente distinta.
Para ilustrarlo vamos a hacer una simulación como la anterior; pero esta vez, habrá tres objetos móviles (uno rojo, uno verde y uno azul). Los tres objetos estarán en la misma posición, pero con una diferencia de 0.001 píxeles. Esta diferencia, provocará que con el tiempo, los tres objetos sigan trayectorias completamente distintas.
comenzar simulación
La vida es un propio ejemplo de sistema caótico. A veces pensamos que ya hemos vivido situaciones similares a las que estamos viviendo en un momento dado; y creemos que la experiencia pasada nos puede servir, pensando que ya sabemos qué va a ocurrir. Pero en realidad, cualquier mínimo detalle puede ser determinante para que la evolución de sucesos sea completamente distinta.
De los sistemas caóticos como este viene “la teoría del caos”; y la famosa metáfora de la mariposa que bate sus alas y cambia radicalmente los acontecimientos futuros en una suerte de efecto dominó cuyas consecuencias se van amplificando. Es una forma de decir; que el más mínimo detalle es crucial para la evolución del sistema.
NOTA: Los sistemas caóticos, a pesar de su nombre, no son azarosos en absoluto; son completamente deterministas.
Atractores
Los atractores, como mención importante (fuera de los propósitos de esta entrada), son sistemas complejos y o caóticos, pero, en los que las trayectorias próximas permanecen siempre próximas, siento permisivos con ciertas perturbaciones en sus condiciones iniciales y evolución.
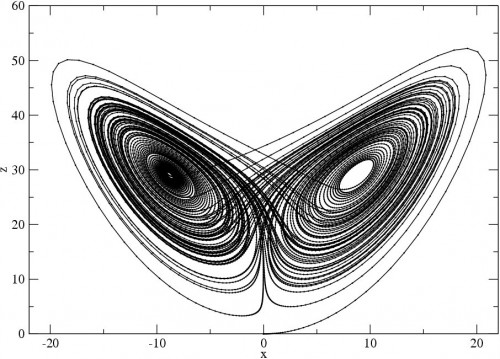
A todos os sonará el más famoso de todos: el atractor de Lorenz (prometo dedicar una entrada para hablar exclusivamente de atractores ;))
El código
Propongo como ejercicio escribir un sistema de simulación como el que hemos usado en esta entrada. Lo único un poco más complicado (sigue siendo sencillo) es hacer las estelas que se van difumando.
Si queréis la solución directa, mi código, con una inicialización de ejemplo que ejecuta una simulación con 25 atractores y 150 objetos móviles (todos aleatorios) es:
function Attractor(canvas)
{
//-[utils]---------------- *********************************************
function randChannel() {return Math.floor(Math.random()*255)}
function randPosition() {return [Math.random()*canvas.width,Math.random()*canvas.height]}
//-[balls]---------------- *********************************************
function Ball(x, y, mass, rgb)
{
//-{init}
this.x=x || randPosition()[0];
this.y=y || randPosition()[1];
this.mass=mass || 4;
this.vx=0;
this.vy=0;
this.radius=this.mass/2;
if(rgb)
this.color="rgb("+rgb[0]+","+rgb[1]+","+rgb[2]+")";
else
this.color="rgb("+randChannel()+","+randChannel()+","+randChannel()+")";
balls.push(this);
//-{methods}
this.move=function()
{
var tmp_vx=0;
var tmp_vy=0;
for(var i=0;i<acelerators.length;i++)
{
var dx=acelerators[i].x-this.x;
var dy=acelerators[i].y-this.y;
var theta=Math.atan2(dy,dx);
var mod=Math.sqrt(Math.pow(dx,2)+Math.pow(dy,2));
var force=Math.min(acelerators[i].force/Math.pow(mod,2),3);
tmp_vx+=force*Math.cos(theta);
tmp_vy+=force*Math.sin(theta);
}
this.vx+=tmp_vx/this.mass;
this.vy+=tmp_vy/this.mass;
this.x+=this.vx;
this.y+=this.vy;
}
this.render=function()
{
current_ctx.save();
current_ctx.fillStyle=this.color;
current_ctx.beginPath();
current_ctx.arc(this.x, this.y, this.radius, 0, 2*Math.PI, false);
current_ctx.closePath();
current_ctx.fill();
current_ctx.restore();
}
}
//-[acelerator]---------------- *********************************************
function Accelerator(x, y, force)
{
//-{init}
this.x=x || randPosition()[0];
this.y=y || randPosition()[1];
this.force=force || 200;
this.radius=this.force/50;
acelerators.push(this);
//-{methods}
this.render=function()
{
ctx.save();
ctx.fillStyle="#000";
ctx.beginPath();
ctx.arc(this.x, this.y, this.radius, 0, 2*Math.PI, false);
ctx.closePath();
ctx.fill();
ctx.restore();
}
}
//-[attractor]----------- *********************************************
//-[setup]----------------
var ctx=canvas.getContext("2d"); //main context
var balls=[]; //balls array
var acelerators=[]; //acelerators array
//-[wake]-----------------
var wake_resolution=20; //number of canvas for the wake
var ctx_buffer=[]; //context array for the wake
var current_ctx=0; //current context object
var arrow=0; //pointer to the current context
var wake_time=2000/wake_resolution; //5 seconds of wake
var last_timestamp=0; //last time of buffer change
var frames=0; //frame count
//-[init]-----------------
for(var i=0;i<wake_resolution;i++)
{
var tmp_canvas=document.createElement("canvas");
tmp_canvas.width=canvas.width;
tmp_canvas.height=canvas.height;
ctx_buffer[i]=tmp_canvas.getContext("2d");
}
current_ctx=ctx_buffer[0];
//-[run]------------------
this.run=function()
{
frames++;
ctx.clearRect(0,0,canvas.width,canvas.height);
//chance of change current context
var now=Date.now();
if(now-last_timestamp>wake_time)
{
last_timestamp=now;
current_ctx=ctx_buffer[(++arrow%ctx_buffer.length)];
current_ctx.clearRect(0,0,canvas.width,canvas.height);
}
//render balls at current context
for(var i=0;i<balls.length;i++)
{
balls[i].move();
balls[i].render();
}
//composition of the wake at main context
var step_alpha=1/ctx_buffer.length;
for(var i=1;i<=ctx_buffer.length;i++)
{
var tmp_ctx=ctx_buffer[(arrow+i)%ctx_buffer.length];
ctx.save();
ctx.globalAlpha=i*step_alpha;
ctx.drawImage(tmp_ctx.canvas,0,0);
ctx.restore();
}
//render acelerators at main context
for(var i=0;i<acelerators.length;i++)
acelerators[i].render();
}
//-[stop]-----------------
this.stop=function()
{
clearInterval(this.id_int); //external setter
}
//-[classes]-----------------
this.Ball=Ball;
this.Accelerator=Accelerator;
}
//gogogo!
(function gogogo()
{
var attractor=new Attractor(canvas);
for(var i=0;i<25;i++)
new attractor.Accelerator();
for(var i=0;i<150;i++)
new attractor.Ball();
attractor.id_int=setInterval(function(){attractor.run()},60/1000); //run at 60 fps
}());
Más simulaciones
Sistema aleatorio con 10 atractores y 20 objetos móviles:
reiniciar simulación aleatoria
Dedicatoria
Esta entrada está dedicada a Virgy; que me inspiró para escribir el simulador tras una conversación; y que finalmente he aprovechado (al margen de su fin original) para hacer esta entrada 🙂
Leer másAutómatas Celulares: Exposición 0
Un autómata celular (de ahora en adelante, CA) es un modelo matemático de un sistema dinámico cuyos estados evolucionan secuencialmente, de forma discreta (no difusa).
Probablemente encontréis algo similar a esta paupérrima definición en cualquier fragmento de literatura especializada que hable sobre el tema. Y digo paupérrima porque mi generosidad y magnanimidad me obliga a decir algo; como sabéis, en ningún caso la descripción de un fin o de una acción puede ser una definición -dado que, de hecho, hay otros “modelos matemáticos de un sis… blablabla” que encajan perfectamente con esa descripción, pero no son CA’s).
Yo siempre los he llamado “máquinas de estados basadas en memoria”. Examinemos su composición. Un CA está formado por:
1) Un espacio discreto de cualquier número de dimensiones que contendrá las células.
el más simple posible: una ristra de una dimesión
2) Un conjunto de células (en alguno de los estados definidos para el sistema)
dos estados: un ejemplo de “células-bits”
3) Una asociación que defina los vecinos de cada célula; usualmente… los adyacentes.
4) Una serie de reglas, que marcarán la evolución de cada célula.
Con todo esto; cada célula evolucionará dependientemente de sus vecinos e independientemente del resto del sistema; según las reglas que se hayan definido.
Generación 0
Generación 1
Generación 2
Supongamos que queremos que el estado de una célula dependa del estado de sus vecinas y del suyo mismo en la generación anterior. Gráficamente la regla podría representarse así:
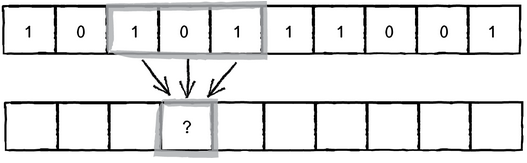
Definimos así 8 reglas, una por cada posibilidad:
El estado final es arbitrario, en este ejemplo hemos elegido éstos porque forman un CA muy simple que genera un resultado muy familiar… 😉
Los CA’s pueden usarse de múltiples formas para realizar cálculos de todo tipo. Un uso muy visual e instructivo para empezar consiste en usar una imagen de dimension W*H, donde W es el número de píxeles de ancho y el número de células del CA, cada fila de píxeles representa el CA en una generación concreta, y la fila siguiente se calcula en base a la anterior hasta un máximo de H generaciones.
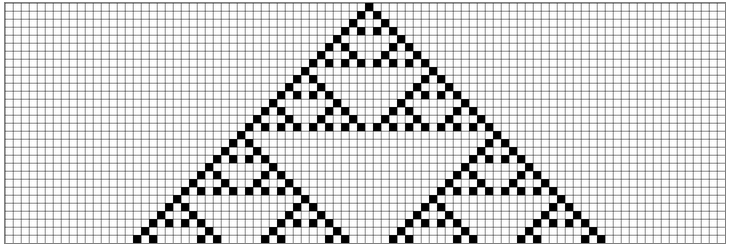
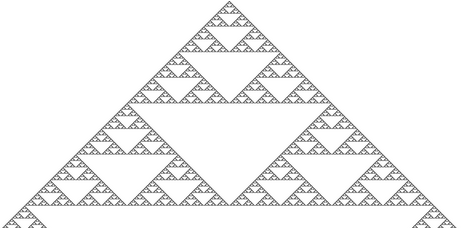
Por ejemplo, si el estado 0 es blanco y el estado 1 es negro, y creamos una imagen con un píxel negro en el centro de la primera fila, al ejecutar nuestro CA de ejemplo para calcular el resto de filas el resultado obtenido es el siguiente:
¿Os suena? Si hacemos un poco de zoom igual lo veis mejor… 😉
Efectivamente, es el triángulo de Sierpiński. Un fractral simple y muy conocido basado en división triangular; aunque nosotros lo hemos generado desde un CA…
Este es un ejemplo simple y rápido de cómo los CA’s pueden ayudarnos a sistematizar con un mínimo esfuerzo… modelos que se repiten en la propia naturaleza 🙂
Un hogar de cera y miel
Este problema lo propuse el 20 de abril en Twitter. Mientras estaba en la playa. Es un problema muy sencillo, aunque sólo una persona de mi TL logró resolverlo… ( @erful )
Problema: En una teselación hexagonal regular, ¿cuál es la distancia entre dos circuncentros adyacentes en función del radio de una circunferencia cincunscrita a uno de los hexágonos?
* Sólo se necesitan matemáticas de la ESO… aunque sorprendente pocos acaban llegando a la solución correcta.
Problema (extra): Utiliza la solución para escribir una función en cualquier lenguaje de programación para dibujar sobre un buffer, plano, canvas, textura… una teselación como la del problema (dimensiones arbitrarias NxM).
* La solución la publicaré el domingo.
Leer más