Autómatas Celulares: Exposición 0
Un autómata celular (de ahora en adelante, CA) es un modelo matemático de un sistema dinámico cuyos estados evolucionan secuencialmente, de forma discreta (no difusa).
Probablemente encontréis algo similar a esta paupérrima definición en cualquier fragmento de literatura especializada que hable sobre el tema. Y digo paupérrima porque mi generosidad y magnanimidad me obliga a decir algo; como sabéis, en ningún caso la descripción de un fin o de una acción puede ser una definición -dado que, de hecho, hay otros “modelos matemáticos de un sis… blablabla” que encajan perfectamente con esa descripción, pero no son CA’s).
Yo siempre los he llamado “máquinas de estados basadas en memoria”. Examinemos su composición. Un CA está formado por:
1) Un espacio discreto de cualquier número de dimensiones que contendrá las células.
![]()
el más simple posible: una ristra de una dimesión
2) Un conjunto de células (en alguno de los estados definidos para el sistema)
![]()
dos estados: un ejemplo de “células-bits”
3) Una asociación que defina los vecinos de cada célula; usualmente… los adyacentes.
4) Una serie de reglas, que marcarán la evolución de cada célula.
Con todo esto; cada célula evolucionará dependientemente de sus vecinos e independientemente del resto del sistema; según las reglas que se hayan definido.
Generación 0
Generación 1
Supongamos que queremos que el estado de una célula dependa del estado de sus vecinas y del suyo mismo en la generación anterior. Gráficamente la regla podría representarse así:
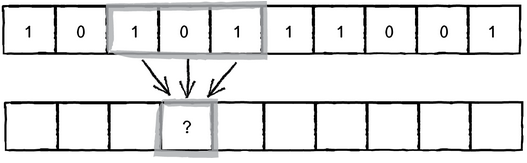
Definimos así 8 reglas, una por cada posibilidad:
El estado final es arbitrario, en este ejemplo hemos elegido éstos porque forman un CA muy simple que genera un resultado muy familiar… 😉
Los CA’s pueden usarse de múltiples formas para realizar cálculos de todo tipo. Un uso muy visual e instructivo para empezar consiste en usar una imagen de dimension W*H, donde W es el número de píxeles de ancho y el número de células del CA, cada fila de píxeles representa el CA en una generación concreta, y la fila siguiente se calcula en base a la anterior hasta un máximo de H generaciones.
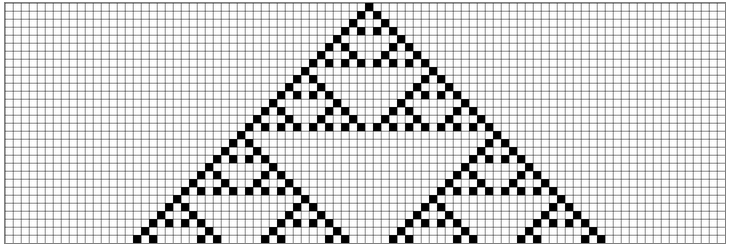
Por ejemplo, si el estado 0 es blanco y el estado 1 es negro, y creamos una imagen con un píxel negro en el centro de la primera fila, al ejecutar nuestro CA de ejemplo para calcular el resto de filas el resultado obtenido es el siguiente:
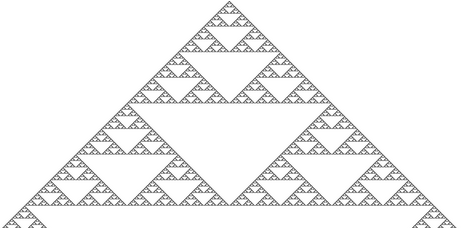
¿Os suena? Si hacemos un poco de zoom igual lo veis mejor… 😉
Efectivamente, es el triángulo de Sierpiński. Un fractral simple y muy conocido basado en división triangular; aunque nosotros lo hemos generado desde un CA…
Este es un ejemplo simple y rápido de cómo los CA’s pueden ayudarnos a sistematizar con un mínimo esfuerzo… modelos que se repiten en la propia naturaleza 🙂