Entradas por: LaNsHoR
Octarino
Arthur C. Clarke
Leer másAtractores, caos, sistemas complejos y mariposas
Siempre nos sentimos más cómodos con aquello que creemos que conocemos; con aquello que ya sabemos y no puede cambiar. Pero en en realidad, siendo un poco puristas, la estabilidad no existe. Ningún sistema en la naturaleza (sistemas reales, no artefactos matemáticos imaginarios) es estable; en el sentido de que no va a permanecer inalterado para siempre. No existe nada en este universo, que haya detenido su evolución nunca.
En la práctica, cuando hacemos ciencia y estudiamos sistemas “aislados”, rebajamos considerablemente nuestros requisitos de estabilidad; y decimos que un sistema ha alcanzado la estabilidad cuando su evolución cesa durante “un tiempo lo suficientemente largo”.
Sí, es tan poco riguroso como suena…
Pero lo divertido está en la incertidumbre, y una vez perdemos el miedo a lo desconocido podemos empezar a disfrutar de ella. Veamos algunos tipos de sistemas con ejemplos sencillos y clasifiquémoslos:
Sistemas Simples
Un ejemplo de sistema simple es una taza de café caliente suspendida en una atmósfera de aire. Poco a poco la taza irá enfriándose hasta alcanzar la temperatura ambiente del aire (el sistema alcanzará la estabilidad). En sus inicios, el sistema no es estable, pero nos sentimos casi tan cómodos con estos sistemas como con los estables porque es fácil predecir su evolución.
Sistemas Complejos
Un sistema complejo es un sistema cuya evolución es muy difícil de determinar; ya que existen factores no evidentes que afectan de forma dramática a cómo evoluciona el sistema. Un ejemplo es el campo gravitatorio, cuando hay varios cuerpos en juego y en movimiento; es difícil calcular la evolución de las trayectorias.
Para verlo mejor; he escrito un pequeño script para hacer simulaciones (del que hablaremos después). En la primera simulación tendréis 6 puntos negros que representan cuerpos “fijos” que atraen a otro “móvil” cuya trayectoria queda marcada por una estela azul. La simulación es infinita y no se estabiliza nunca (aunque durante un rato el objeto móvil se salga de la pantalla, tarde o temprano volverá).
Para empezar la simulación haced clic en “empezar simulación” (podéis reiniciarla cuando queráis). ¿Podéis calcular mentalmente su trayectoria (la evolución del sistema)? Entonces, es un sistema complejo. Otro ejemplo de sistema complejo es el clima de la tierra.
Sistemas Caóticos
Un sistema caótico es un sistema, que además de complejo, cumple la siguiente propiedad fundamental: un mínimo y casi insignificante cambio en las condiciones iniciales hace que el sistema evolucione de forma radicalmente distinta.
Para ilustrarlo vamos a hacer una simulación como la anterior; pero esta vez, habrá tres objetos móviles (uno rojo, uno verde y uno azul). Los tres objetos estarán en la misma posición, pero con una diferencia de 0.001 píxeles. Esta diferencia, provocará que con el tiempo, los tres objetos sigan trayectorias completamente distintas.
comenzar simulación
La vida es un propio ejemplo de sistema caótico. A veces pensamos que ya hemos vivido situaciones similares a las que estamos viviendo en un momento dado; y creemos que la experiencia pasada nos puede servir, pensando que ya sabemos qué va a ocurrir. Pero en realidad, cualquier mínimo detalle puede ser determinante para que la evolución de sucesos sea completamente distinta.
De los sistemas caóticos como este viene “la teoría del caos”; y la famosa metáfora de la mariposa que bate sus alas y cambia radicalmente los acontecimientos futuros en una suerte de efecto dominó cuyas consecuencias se van amplificando. Es una forma de decir; que el más mínimo detalle es crucial para la evolución del sistema.
NOTA: Los sistemas caóticos, a pesar de su nombre, no son azarosos en absoluto; son completamente deterministas.
Atractores
Los atractores, como mención importante (fuera de los propósitos de esta entrada), son sistemas complejos y o caóticos, pero, en los que las trayectorias próximas permanecen siempre próximas, siento permisivos con ciertas perturbaciones en sus condiciones iniciales y evolución.
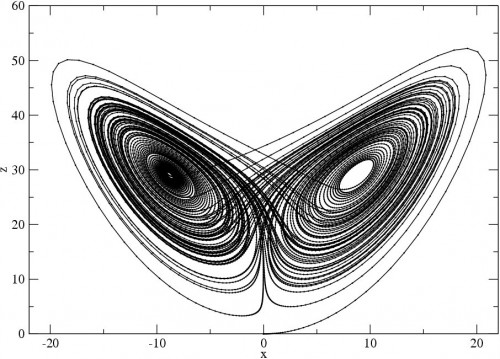
A todos os sonará el más famoso de todos: el atractor de Lorenz (prometo dedicar una entrada para hablar exclusivamente de atractores ;))
El código
Propongo como ejercicio escribir un sistema de simulación como el que hemos usado en esta entrada. Lo único un poco más complicado (sigue siendo sencillo) es hacer las estelas que se van difumando.
Si queréis la solución directa, mi código, con una inicialización de ejemplo que ejecuta una simulación con 25 atractores y 150 objetos móviles (todos aleatorios) es:
function Attractor(canvas)
{
//-[utils]---------------- *********************************************
function randChannel() {return Math.floor(Math.random()*255)}
function randPosition() {return [Math.random()*canvas.width,Math.random()*canvas.height]}
//-[balls]---------------- *********************************************
function Ball(x, y, mass, rgb)
{
//-{init}
this.x=x || randPosition()[0];
this.y=y || randPosition()[1];
this.mass=mass || 4;
this.vx=0;
this.vy=0;
this.radius=this.mass/2;
if(rgb)
this.color="rgb("+rgb[0]+","+rgb[1]+","+rgb[2]+")";
else
this.color="rgb("+randChannel()+","+randChannel()+","+randChannel()+")";
balls.push(this);
//-{methods}
this.move=function()
{
var tmp_vx=0;
var tmp_vy=0;
for(var i=0;i<acelerators.length;i++)
{
var dx=acelerators[i].x-this.x;
var dy=acelerators[i].y-this.y;
var theta=Math.atan2(dy,dx);
var mod=Math.sqrt(Math.pow(dx,2)+Math.pow(dy,2));
var force=Math.min(acelerators[i].force/Math.pow(mod,2),3);
tmp_vx+=force*Math.cos(theta);
tmp_vy+=force*Math.sin(theta);
}
this.vx+=tmp_vx/this.mass;
this.vy+=tmp_vy/this.mass;
this.x+=this.vx;
this.y+=this.vy;
}
this.render=function()
{
current_ctx.save();
current_ctx.fillStyle=this.color;
current_ctx.beginPath();
current_ctx.arc(this.x, this.y, this.radius, 0, 2*Math.PI, false);
current_ctx.closePath();
current_ctx.fill();
current_ctx.restore();
}
}
//-[acelerator]---------------- *********************************************
function Accelerator(x, y, force)
{
//-{init}
this.x=x || randPosition()[0];
this.y=y || randPosition()[1];
this.force=force || 200;
this.radius=this.force/50;
acelerators.push(this);
//-{methods}
this.render=function()
{
ctx.save();
ctx.fillStyle="#000";
ctx.beginPath();
ctx.arc(this.x, this.y, this.radius, 0, 2*Math.PI, false);
ctx.closePath();
ctx.fill();
ctx.restore();
}
}
//-[attractor]----------- *********************************************
//-[setup]----------------
var ctx=canvas.getContext("2d"); //main context
var balls=[]; //balls array
var acelerators=[]; //acelerators array
//-[wake]-----------------
var wake_resolution=20; //number of canvas for the wake
var ctx_buffer=[]; //context array for the wake
var current_ctx=0; //current context object
var arrow=0; //pointer to the current context
var wake_time=2000/wake_resolution; //5 seconds of wake
var last_timestamp=0; //last time of buffer change
var frames=0; //frame count
//-[init]-----------------
for(var i=0;i<wake_resolution;i++)
{
var tmp_canvas=document.createElement("canvas");
tmp_canvas.width=canvas.width;
tmp_canvas.height=canvas.height;
ctx_buffer[i]=tmp_canvas.getContext("2d");
}
current_ctx=ctx_buffer[0];
//-[run]------------------
this.run=function()
{
frames++;
ctx.clearRect(0,0,canvas.width,canvas.height);
//chance of change current context
var now=Date.now();
if(now-last_timestamp>wake_time)
{
last_timestamp=now;
current_ctx=ctx_buffer[(++arrow%ctx_buffer.length)];
current_ctx.clearRect(0,0,canvas.width,canvas.height);
}
//render balls at current context
for(var i=0;i<balls.length;i++)
{
balls[i].move();
balls[i].render();
}
//composition of the wake at main context
var step_alpha=1/ctx_buffer.length;
for(var i=1;i<=ctx_buffer.length;i++)
{
var tmp_ctx=ctx_buffer[(arrow+i)%ctx_buffer.length];
ctx.save();
ctx.globalAlpha=i*step_alpha;
ctx.drawImage(tmp_ctx.canvas,0,0);
ctx.restore();
}
//render acelerators at main context
for(var i=0;i<acelerators.length;i++)
acelerators[i].render();
}
//-[stop]-----------------
this.stop=function()
{
clearInterval(this.id_int); //external setter
}
//-[classes]-----------------
this.Ball=Ball;
this.Accelerator=Accelerator;
}
//gogogo!
(function gogogo()
{
var attractor=new Attractor(canvas);
for(var i=0;i<25;i++)
new attractor.Accelerator();
for(var i=0;i<150;i++)
new attractor.Ball();
attractor.id_int=setInterval(function(){attractor.run()},60/1000); //run at 60 fps
}());
Más simulaciones
Sistema aleatorio con 10 atractores y 20 objetos móviles:
reiniciar simulación aleatoria
Dedicatoria
Esta entrada está dedicada a Virgy; que me inspiró para escribir el simulador tras una conversación; y que finalmente he aprovechado (al margen de su fin original) para hacer esta entrada 🙂
Leer másLa visión en los perros
Llevo tiempo preguntándome cómo se ve el mundo desde los ojos de Arthur. Algunas personas piensan que los perros ven en blanco y negro, pero lo cierto es que sí distinguen algunos colores. En concreto, perros, lobos, zorros… y la mayoría de los cánidos y mamíferos poseen una forma de visión dicromática llamada deuteranopía; y es también, de hecho, una forma de daltonismo en humanos.
Los colores
Para entender nuestra visión: en la retina humana (y en la de muchos primates) podemos encontrar bastones (células de visión por intensidad) y tres tipos de conos (células responsables de la visión en color); cada tipo de cono especializado en una longitud de onda diferente: “azules” sensibles en un rango de longitudes centradas en el azul (unos 430nm), “verdes” especializados en longitudes de onda similares a la del verde (unos 520nm) y “rojos” para longitudes de onda largas cercanas al rojo (~650nm).
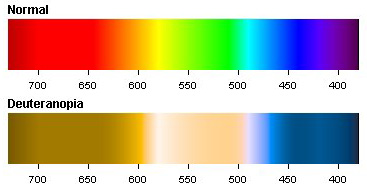
Dado que estas son las longitudes de los colores primarios aditivos (rojo – verde- azul); la composición de la información receptada por cada tipo de cono completa un espectro como el siguiente:
En los animales con deuteranopía los conos responsables de la recepción del verde no están presentes o no son funcionales. La composición de la información receptada presenta en estos casos un espectro como el siguiente:
Niveles de gris
Otra diferencia importante entre la visión humana y la de un perro es la diferencia mínima perceptible entre factores de gris (AR). Para esta medición se suele usar la ley de Weber-Fechner; una regla psicofísica que establece una relación cuantitativa entre la magnitud de un estímulo físico y cómo éste es percibido. El resultado de la fracción de Webber para humanos se estima en 0.11, y para perros en 0.22; esto significa que los perros son sólo capaces de captar la mitad de niveles de grises que nosotros.
Por ejemplo, los perros verían los siguientes cuadrados del mismo color:
Si tú ves el mismo color en ambos cuadrados, puede deberse a que tu monitor sea de gama baja y no sea capaz de mostrar correctamente los colores (o que esté mal configurado en parámetros de brillo, contraste y temperatura). Descartamos la opción de que seas un perro, claro.
Agudeza visual
Dicho en pocas (pero muy imprecisas) palabras; la agudeza visual es la resolución espacial del sistema visual. Al tratarse de un término de resolución es fácil imaginar que está directamente relacionado con la densidad de conos y bastones de la retina. Esta densidad varía según la zona; así, perdemos resolución en los límites de nuestro campo visual (donde apenas podemos percibir objetos) y alcanzamos el máximo en el punto donde centramos la vista.
El máximo de agudeza visual para humanos está entre 50 y 60 CPD. En los perros se sitúa entre 6.5-9 y 11.6 CPD.
Simular cómo es la visión con una agudeza visual diferente a la nuestra es complicado; intervienen muchos factores y es alterada circunstancialmente por el entorno. Por ejemplo el desenfoque por profundidad de campo se dispara (no podemos simularlo en una imagen 2D) al enfocar; y la cantidad de luz recibida también afecta de forma virtual; ya que los perros tienen mayor densidad de bastones que los humanos, pupilas más grandes y un tapetum lucidum refractivo; así en la oscuridad la agudeza visual de los perros acabaría superando a la del humano.
Aunque esta aproximación sea muy imprecisa; podemos ilustrar la pérdida de resolución con la siguiente figura; asumiendo un factor de /4 para los perros.
AV /1
AV /4
Al lío. Dedos al código.
Con todo este resumen; la idea es escribir una pequeña función javascript que dada una imagen de ejemplo la transforme y haga una aproximación acertada de cómo la percibiría un perro.
La función tiene 3 tareas independiente a realizar:
1) Simulación de deuterapía: No es tan sencillo como pueda parecer, ya que los niveles de luz y ponderaciones entre colores cambian gradualmente según la curva de sensibilidad de los conos que sí están presentes (rojo-azul). En este paper [1] encontramos los factores medidos experimentalmente -para humanos; aunque la diferencia con perros es mínima (comparamos con [2])- que necesitaremos para la conversión.
2) Discretizamos algunos niveles de luz. No vamos a implementar todas las curvas; sólo una aproximación. Algo de información adicional en [3]. Hacemos una reducción de la intensidad a niveles pares.
3) Desenfoque gausiano a la imagen. Para hacerlo correctamente el desenfoque variaría su grado arbitrariamente según la zona; y para ello necesitaríamos una imagen tridimensional, información sobre la exposición y el punto de enfoque marcado. Como no tenemos nada de eso, hacemos un desenfoque suave y global que simule el máximo grado de agudeza visual en todos los puntos. El desenfoque podemos hacerlo eficientemente (usando la GPU) mediante un filtro en CSS3 (fuera del código javascript).
function DogVision() //v0.1 - LaNsHoR @ 2014
{
//===================================================
//Factors
var gamma=1.0 /* normal value: 1.8;
-0.8 correction for dogs */
var by=127, k=[9591, 23173, -730];
for(var luts={}, invluts={}, i=0; i<256; i++)
{
luts[i]=0.992052*Math.pow(i/255, gamma)+0.003974;
invluts[i]=255*Math.pow(i/255, 1/1.8);
}
//===================================================
//Functions
//-- RGB normalization
function normalize(value)
{return value<0?0:value>255?255:value;}
//-- Dog light reduction
function even(value) {return value%2?value-1:value;}
//===================================================
this.dogPixel=function(r,g,b)
{
var r_lin=luts[r], g_lin=luts[g], b_lin=luts[b];
var r_blind=((k[0]*r_lin)+(k[1]*g_lin))/by;
var b_blind=((k[2]*r_lin)-(k[2]*g_lin)+32768*b_lin)/by;
r_blind=normalize(r_blind);
b_blind=normalize(b_blind);
var red=invluts[Math.round(r_blind)];
var blue=blue=invluts[Math.round(b_blind)];
return [even(red), even(red), even(blue)];
}
}
Y ya está! Podemos empezar a jugar con los resultados 🙂
Ejemplos
El resultado aparecerá en el rectángulo de borde azul.
Conclusión de andar por casa
Por todo lo dicho y visto; los perros en ambientes de luz diurna tienen una visión mucho más precaria que la humana. Sin embargo, con condiciones de baja luz su percepción de siluetas es mucho mejor que la nuestra (fijaos en los ejemplos). Además, su mayor número de bastones les hacen mejores detectando pequeños movimientos a grandes distancias (algo que no podemos percibir en imágenes estáticas).
No está nada mal. Después de todo; su sentido principal es el olfato (la mayoría de neuronas de su corteza cerebral están dedicadas a este sentido; la mayoría de las nuestras, a la visión). Aún con una visión mediocre, si sumamos sus excelentes olfato y oído su nivel de percepción sensorial global es superior al nuestro. Y desde luego, perfectamente adaptado a lo que necesitan.
Dedicatoria
Esta entrada y el código fuente de la función que hemos escrito están dedicados a Quarkyta… una de las preciosas perritas de Virgy, que nos dejó hace unos días 🙁
Referencias
[1] Digital Video Colourmaps for Checking the Legibility of Displays by Dichromats
[3] The spectral luminosity curves for a dichroma tic eye and a normal eye
Leer más
A salvo de errores… o quizá no
StormByte me ha mandado este problema para vosotros, yo esperaré un par de días y después participaré también! 🙂
Problema:
PHP es un lenguage muy dinámico, tanto, que te permite hacer muchas cosas, algunas buenas, algunas documentadas, y otras, no tan buenas y no tan documentadas.
En este caso, hablaremos del gancho (hook) que PHP pone a nuestra disposición para manejar los posibles errores con los que nos podamos encontrar y evitar que salga una advertencia que nos estropee la página.
Se trata de:
mixed set_error_handler ( callable $error_handler [,
int $error_types = E_ALL | E_STRICT ] )
Que establece una función de usuario (error_handler) para manejar los errores de un script.
Su uso es muy sencillo, y nos permite estar a salvo de los errores que se nos puedan presentar (junto con error_reporting(0))
Este es el codigo:
<?php
error_reporting(0);
function erroresBonitos($errno, $errstr, $errfile, $errline) {
//Manejar errores aquí, mandar un email, etc
}
set_error_handler("erroresBonitos", E_ALL);
if ($t[0])
{
/* no se ejecuta, pero causará un warning que el
handler maneja perfectamente sin romper nuestra web */
}
//Y finalmente, nuestra web en su bonito HTML, etc
echo "Test Mi pagina";
?>
Con esto, estaríamos a salvo de los errores que se nos puedan presentar, podríamos enviar un email al admin web, guardar el error en la base de datos, e incluso decirle al usuario que nos contacte, pero… ¿estamos seguros del todo?
La respuesta es NO, aún quedan algunos casos para los que no estamos protegidos, y para poder confiar en un handler de errores, tiene que manejar el 100% de los casos.
Con lo que este problema tiene 2 preguntas:
1.- ¿Qué podría ir mal y “saltarse” este handler de errores?
2.- ¿Podríamos protegernos de los casos de la pregunta 1 de alguna forma? Si es así, ¿Cómo podríamos hacerlo?
Esperamos unos días como de costumbre, y si no aparecen respuestas o van muy desencaminadas desvelamos la primera y dejamos algo más de tiempo para la segunda.
Leer más